Auch wenn das Vertrauen in die Erkenntnisse der Naturwissenschaft in diesen Zeiten so unaufhörlich wie die arktischen Polkappen schmilzt, bleibt ihre Publikation eine der wichtigsten und zugleich anspruchvollsten Aufgaben von Verlagen. Neben großformatigen Tabellen und epischen Literaturapparaten sind es vor allem mathematische Formeln, die typografisch und technisch hohe Anforderungen an ihren Satz stellen.
Leider finden sich aber häufig Unschönheiten in Manuskripten, Daten und Drucksachen, die oft auf ein fehlendes Verständnis der Grundregeln des Formelsatzes zurückzuführen sind. Ohne diese typografischen Grundregeln lässt sich aber weder die Qualität des Satzes, noch ihre digitale Datenform wirklich beurteilen. Daher widmet sich der vorliegende Beitrag zunächst der Typografie mathematischer Formeln und ihrer Bedeutung, ehe wir uns im Anschluss den Problemen der Digitalisierung von Formeln widmen.
Das Fundament dieser Regeln bildet das Système international d’unités (SI), auf dem auch deutsche Normen wie die DIN 1338 fußen. Im SI wird nicht nur ein System für physikalische Einheiten, sondern auch typografische Konventionen für den richtigen Satz von Einheiten, Symbolen und numerischen Werten festgelegt, die Missverständnissen beim Lesen und Verstehen von Formeln vorbeugen sollen.
Selbstredend spielt schon die Groß- und Kleinschreibung eine entscheidende Rolle, Laut SI werden Einheiten klein geschrieben, außer sie sind von Eigennamen wie Joule oder Pascal abgeleitet. Eine besondere Ausnahme bildet die Einheit Liter, um eine Verwechslung der Zahl „1“ mit dem kleinen „l“ zu vermeiden. Funktionsnamen wie etwa sin, cos und tan schreibt man klein, dagegen hält man sich bei Größensymbolen an die qua Herkunft überlieferte Schreibweise.
Manche Autoren machen den Fehler, aus ästhetischen Gesichtspunkten alle Formeln einheitlich in einem ihnen ansprechenden Schriftschnitt zu schreiben. Doch schon die Gleichung m = 2g ist nicht gleichbedeutend mit m = 2g. Erstere Formel würde man also als Masse gleich zwei Gramm lesen, während man letztere als Masse gleich das Produkt aus zwei und der Fallbeschleunigung missverstehen könnte, was freilich physikalisch wenig Sinn macht.
Das SI sieht vor, Einheiten wie Gramm steil zu setzen, während Größensymbole – dazu zählen auch technische und physikalische Konstanten wie die Fallbeschleunigung – kursiviert werden. Mathematische Konstanten wie π oder die Eulersche Zahl e, numerische Werte, Operatoren, Funktionsnamen sowie Elemente und Elementarteilchen wie H2O setzt man dagegen stets aufrecht. In diesem Sinne wird der griechische Buchstabe μ als Zeichen der reduzierten Masse μ kursiv gesetzt, hingegen bleibt er beim Elementarteilchen Myon (μ) und der Gewichtsangabe in Mikrogramm (µg) steil.
Um Vektoren (gerichtete Größen) wie Kraft und Beschleunigung von skalaren (ungerichteten) Größen wie Masse und Druck zu unterscheiden, ist es üblich, diese entweder halbfett und kursiv oder nur kursiv mit einen Pfeil über dem Buchstaben auszuzeichnen.
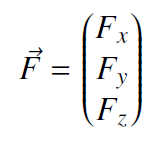
Nicht von der SI vorgeschrieben, aber dennoch wichtig ist der richtige Einsatz von Weißraum in Formeln. Mitunter werden Formeln so dicht gedrängt gesetzt, dass ihnen buchstäblich der Platz zum Atmen fehlt. So lässt man um Operatoren wenigstens einen Wortabstand Platz, sofern diese nicht als Vorzeichen gelten.
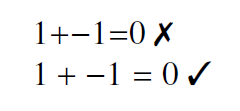
Was die Satzart betrifft, so richtet man mathematische Formeln üblicherweise an der Mittelachse oder seltener von der Satzkante linksbündig abgesetzt aus. Falls eine Gleichung in mehreren Zeilen umgestellt wird, so wird diese am Gleichheitszeichen ausgerichtet:
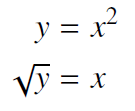
Beim Umbruch von Gleichungen mit mehreren Teilen verwendet man auch das Gleichheitszeichen zur Ausrichtung. Dabei steht das folgende Gleichheitszeichen unter dem vorherigen.
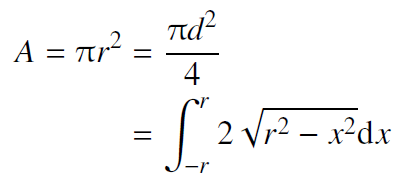
Ansonsten kann man mathematische Formeln auch an Operatoren teilen, wobei der Operator aber immer mit auf die nächste Zeile umbrochen wird. Ausdrücke in Klammern versucht man immer zusammenzuhalten.
Zudem gibt es Besonderheiten, wenn Formeln in eine Textzeile eingebettet (inline) oder abgesetzt in einem eigenen Absatz stehen (display). Zunächst sollte der Schriftgrad der Inline-Formel immer dem der der Grundschrift entsprechen und die vertikale Ausrichtung sollte an der Grundlinie der Textzeile erfolgen.
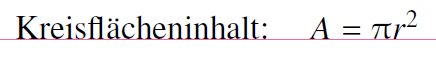
Im Fall von Inline-Formeln werden bei Summenzeichen, Integralen und Grenzwerten die Variablen und Indizes nicht mehr oben und unten sondern rechts neben das Zeichen gesetzt, um die Höhe der Formel zu minimieren:
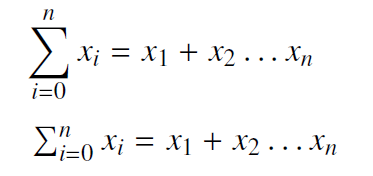
Gleiches gilt auch für Klammern und Brüche. Falls möglich, vermeidet man bei Inline-Formeln die Verwendung von skalierenden Klammern, da sich diese flexibel an die Größe des Inhalts anpassen und mit Ober- oder Unterlängen anderer Zeilen kollidieren können. Stattdessen sollte bei Inline-Formeln die Größe der Klammer der einer regulären Textklammer entsprechen. Zudem setzt man die Zeichen innerhalb eines Bruches kleiner und verringert den vertikalen Weißraum.
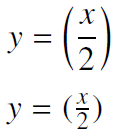
Im Gegensatz zu Inline-Formeln stehen abgesetzte Formeln in einem eigenen Absatz. Sind diese in einen Satz eingebettet, so gelten diese als sein Bestandteil und müssen bei Bedarf mit einem Satzzeichen versehen werden.

Um Formeln an anderer Stelle zu zitieren, werden diese fortlaufend nummeriert. Die Nummer wird für gewöhnlich in Klammern gesetzt und am rechten Rand der Kolumne auf die Grundlinie der Formel platziert. Bei umbrochenen Gleichungen wird die Nummer immer auf der Höhe der letzten Zeile gesetzt.
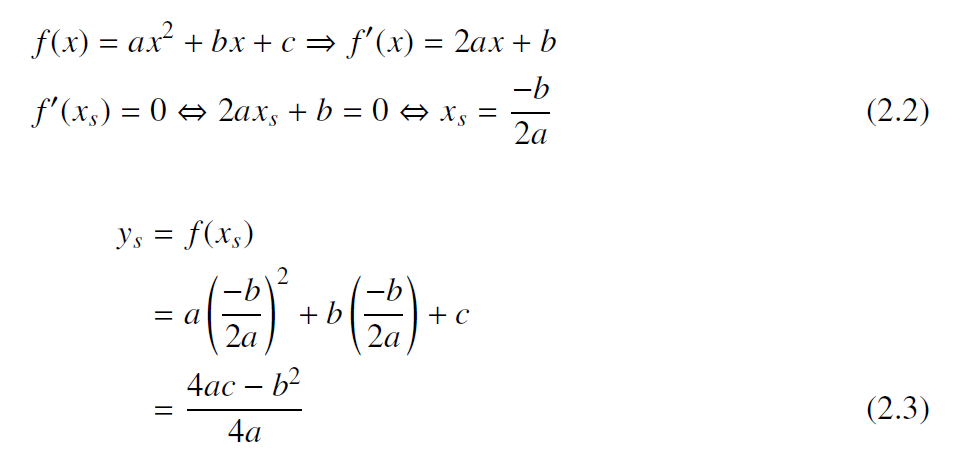
Bei großen Werken bezieht man die Kapitelnummer ein, um das Nachschlagen der Formel zu erleichtern. Zusammengehörige Formeln kann man durch einen zusätzlichen alphabetischem Index kennzeichnen, wie beispielsweise (1a), (1b) usw.
Zum Nachschlagen empfiehlt sich die SI-Broschüre ab Punkt 5, die DIN 1338, über die es auch frei verfügbare Zusammenfassungen im Netz gibt, sowie der Abschnitt „Mathematischer Formelsatz“ im Buch Detailtypografie von Friedrich Forssman und Ralf de Jong. Nach diesem Streifzug durch das Feld des Formelsatzes widme ich mich im kommenden Beitrag, den Möglichkeiten, Formeln zu editieren, zu kodieren und in Print und Web darzustellen bzw. den kleinen und großen Katastrophen, die auf diesem Wege geschehen können.
